最近研究魔方的玩法,就突然想用HMTL5寫一個(gè)魔方的模型,由于魔方是一個(gè)3D的立方體,這次就試著用HTML5寫了一個(gè)簡(jiǎn)單的3D模型。
下面是預(yù)覽畫面。

制作流程
首先你需要下載Html5開(kāi)源庫(kù)件lufylegend-1.4.0
魔方分為6個(gè)面,每個(gè)面由9個(gè)小矩形組成,現(xiàn)在我把每個(gè)小矩形當(dāng)做一個(gè)類封裝起來(lái),
因?yàn)楝F(xiàn)在建立的是一個(gè)3D魔方,所以要畫出每個(gè)小矩形,需要知道小矩形的4個(gè)定點(diǎn),而這4個(gè)定點(diǎn)會(huì)根據(jù)空間的旋轉(zhuǎn)角度而變換,所以為了計(jì)算出這4個(gè)定點(diǎn)坐標(biāo),需要知道魔方繞x軸和z軸旋轉(zhuǎn)的角度。
所以,建立矩形類如下
function Rect(pointA,pointB,pointC,pointD,angleX,angleZ,color){
base(this,LSprite,[]);
this.pointZ=[(pointA[0]+pointB[0]+pointC[0]+pointD[0])/4,(pointA[1]+pointB[1]+pointC[1]+pointD[1])/4,(pointA[2]+pointB[2]+pointC[2]+pointD[2])/4];
this.z = this.pointZ[2];
this.pointA=pointA,this.pointB=pointB,this.pointC=pointC,this.pointD=pointD,this.angleX=angleX,this.angleZ=angleZ,this.color=color;
}
Rect.prototype.setAngle = function(a,b){
this.angleX = a;
this.angleZ = b;
this.z=this.getPoint(this.pointZ)[2];
};
pointA,pointB,pointC,pointD是小矩形的四個(gè)頂點(diǎn),angleX,angleZ分別是x軸和z軸旋轉(zhuǎn)的角度,color是小矩形的顏色。
魔方分為6個(gè)面,先看一下最前面的一面,如果以立方體的中心作為3D坐標(biāo)系的中心,那么9個(gè)小矩形的各個(gè)定點(diǎn)所對(duì)應(yīng)的坐標(biāo)如下圖所示
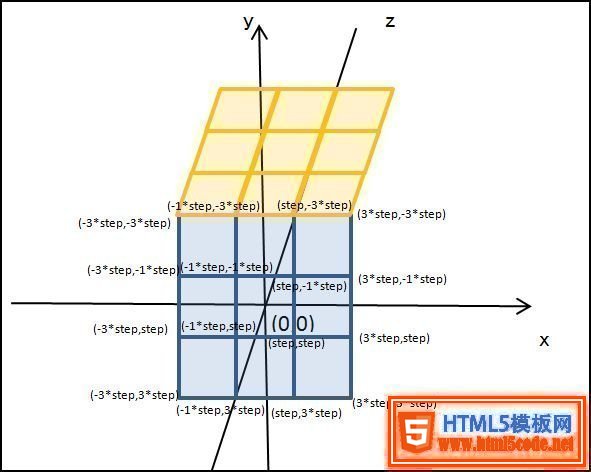
所以,前面這個(gè)面的9個(gè)小矩形可以由下面的代碼來(lái)建立
for(var x=0;x<3;x++){
for(var y=0;y<3;y++){
z = 3;
var rect = new Rect([-3*step + x*2*step,-3*step + y*2*step,-3*step + z*2*step],[-step + x*2*step,-3*step + y*2*step,-3*step + z*2*step],[-step + x*2*step,-step + y*2*step,-3*step + z*2*step],[-3*step + x*2*step,-step + y*2*step,-3*step + z*2*step],0,0,"#FF0000");
backLayer.addChild(rect);
}
}
其中backLayer是一個(gè)LSprite類,step是半個(gè)小矩形的長(zhǎng),同樣的道理,可以也得到其他5個(gè)面。
6個(gè)面都建立了,在繪制這6個(gè)面之前,首先要根據(jù)旋轉(zhuǎn)的角度來(lái)計(jì)算各個(gè)定點(diǎn)的坐標(biāo),看下面的圖
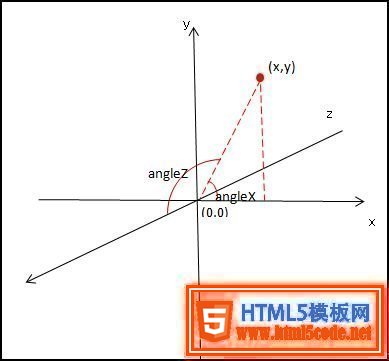
根據(jù)上面的圖,用下面的公式即可得到變換后的定點(diǎn)坐標(biāo)
Rect.prototype.getPoint = function(p){
var u2,v2,w2,u=p[0],v=p[1],w=p[2];
u2 = u * Math.cos(this.angleX) - v * Math.sin(this.angleX);
v2 = u * Math.sin(this.angleX) + v * Math.cos(this.angleX);
w2 = w;
u = u2; v = v2; w = w2;
u2 = u;
v2 = v * Math.cos(this.angleZ) - w * Math.sin(this.angleZ);
w2 = v * Math.sin(this.angleZ) + w * Math.cos(this.angleZ);
u = u2; v = v2; w = w2;
return [u2,v2,w2];
};
最后根據(jù)小矩形的四個(gè)定點(diǎn)坐標(biāo),來(lái)繪制這個(gè)矩形,
Rect.prototype.draw = function(layer){
this.graphics.clear();
this.graphics.drawVertices(1,"#000000",[this.getPoint(this.pointA),this.getPoint(this.pointB),this.getPoint(this.pointC),this.getPoint(this.pointD)],true,this.color);
};
其中drawVertices是lufylegend.js庫(kù)件中LGraphics類的一個(gè)方法,它可以根據(jù)傳入的定點(diǎn)坐標(biāo)數(shù)組來(lái)繪制一個(gè)多邊形。
最后,給出完整代碼,代碼很少,JS代碼一共91行。
一,index.html
<!DOCTYPE html> <html> <head> <meta charset="UTF-8"> <title>3D魔方</title> </head> <body> <div id="mylegend">loading……</div> <script type="text/javascript" src="../lufylegend-1.4.0.min.js"></script> <script type="text/javascript" src="./Main.js"></script> <script type="text/javascript" src="./Rect.js"></script> </body> </html>
二,Rect類
function Rect(pointA,pointB,pointC,pointD,angleX,angleZ,color){
base(this,LSprite,[]);
this.pointZ=[(pointA[0]+pointB[0]+pointC[0]+pointD[0])/4,(pointA[1]+pointB[1]+pointC[1]+pointD[1])/4,(pointA[2]+pointB[2]+pointC[2]+pointD[2])/4];
this.z = this.pointZ[2];
this.pointA=pointA,this.pointB=pointB,this.pointC=pointC,this.pointD=pointD,this.angleX=angleX,this.angleZ=angleZ,this.color=color;
}
Rect.prototype.draw = function(layer){
this.graphics.clear();
this.graphics.drawVertices(1,"#000000",[this.getPoint(this.pointA),this.getPoint(this.pointB),this.getPoint(this.pointC),this.getPoint(this.pointD)],true,this.color);
};
Rect.prototype.setAngle = function(a,b){
this.angleX = a;
this.angleZ = b;
this.z=this.getPoint(this.pointZ)[2];
};
Rect.prototype.getPoint = function(p){
var u2,v2,w2,u=p[0],v=p[1],w=p[2];
u2 = u * Math.cos(this.angleX) - v * Math.sin(this.angleX);
v2 = u * Math.sin(this.angleX) + v * Math.cos(this.angleX);
w2 = w;
u = u2; v = v2; w = w2;
u2 = u;
v2 = v * Math.cos(this.angleZ) - w * Math.sin(this.angleZ);
w2 = v * Math.sin(this.angleZ) + w * Math.cos(this.angleZ);
u = u2; v = v2; w = w2;
return [u2,v2,w2];
};
